8.3.2 SHM Energy in time-domain

If we go with $\displaystyle v=\omega {{x}_{0}}\cos \omega t$ , then we can write $\displaystyle KE=\frac{1}{2}m{{v}^{2}}$ as

$\displaystyle KE=\frac{1}{2}m{{\omega }^{2}}{{x}_{0}}^{2}{{\cos }^{2}}\omega t$

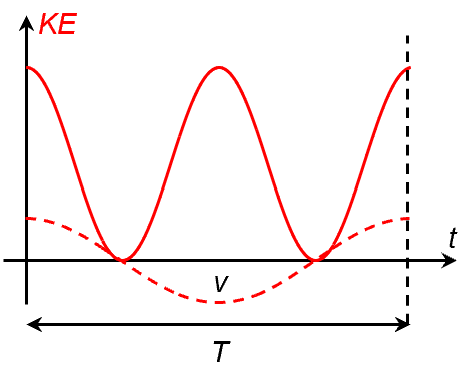
Two energy cycles per oscillation

Notice that there are two complete KE cycles in one velocity cycle. Physically, this is because KE is a scalar whereas velocity is a vector. So the KE is the same regardless whether v is in the positive or negative direction. Mathematically, this is because $\displaystyle {{\cos }^{2}}\omega t=\frac{{1+\cos 2\omega t}}{2}$ , which is a raised sinusoid with frequency 2f.

The PE can be derived from

$\displaystyle \begin{aligned}PE&=TE-KE\\&=\frac{1}{2}m{{\omega }^{2}}{{x}_{0}}^{2}-\frac{1}{2}m{{\omega }^{2}}{{x}_{0}}^{2}{{\cos }^{2}}\omega t\\&=\frac{1}{2}m{{\omega }^{2}}{{x}_{0}}^{2}(1-{{\cos }^{2}}\omega t)\\&=\frac{1}{2}m{{\omega }^{2}}{{x}_{0}}^{2}{{\sin }^{2}}\omega t\end{aligned}$

Similarly, there are two PE cycles in one oscillation cycle because PE is maximum at both the extreme positions, and zero whenever the oscillation crosses the equilibrium position.

For completeness’s sake, we present TE, PE and KE in the same graph below.

Exam Tip

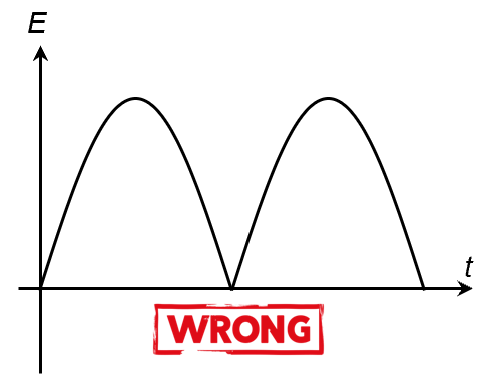
During examinations, students lose marks when they sketch the PE and KE graphs to have the shape of the humpy McDonald’s sign. Do realize that the PE and KE graphs are raised sinusoidal functions. They should thus have the shape of smooth sinusoids.