22P2Q02

2ai)

A quantity that has both magnitude and direction.

2aii)

Velocity

COMMENT: You can also write displacement, force, acceleration, etc

2bi)

\displaystyle \begin{aligned}   mg\sin \theta &=(16)(\sin 35{}^\circ ) \\  &=9.18\text{ N} \end{aligned}

COMMENT: This also means that the friction force must be  9.18 N, since object is moving at constant speed.

2bii)

Since net force is zero:

\displaystyle \begin{aligned}   P&=mg\sin \theta +f \\  &=9.18+9.18 \\  &=18.4\text{ N} \end{aligned}

COMMENT: Note that the frictional force has flipped direction.

2ci)

\displaystyle \begin{aligned}   \text{Impulse }J&=\Delta p \\  &=m\Delta v \\  &=(0.22)(3.5-2.6) \\  &=0.198\text{ N s} \end{aligned}

2cii)

COMMENT: From the fact that X gains speed (and did not switch direction) after the collision, we can deduce that Y was also traveling in the same direction as X before the collision.

Method 1

By PCOM: \displaystyle \begin{aligned}\sum {{p}_{i}}&=\sum {{p}_{f}} \\   0.40\times 3.3+0.22\times 2.6&=0.40\times v+0.22\times 3.5 \\   v&=2.81\text{ m }{{\text{s}}^{-1}}  \end{aligned}

Method 2

\displaystyle \begin{aligned}\Delta p&=m\Delta v \\   -0.198&=(0.40)({{v}_{Y}}-3.3) \\   {{v}_{Y}}&=2.81\text{ m }{{\text{s}}^{-1}}  \end{aligned}

COMMENT: You must not assume the collision to be elastic (hence you must not apply RSOA&=RSOS), since the question did not state so.

2ciii)

Method 1

Distance\displaystyle ={{v}_{average}}\times t=\frac{2.6+3.5}{2}\times 0.2=0.61\text{ m}

Method 2

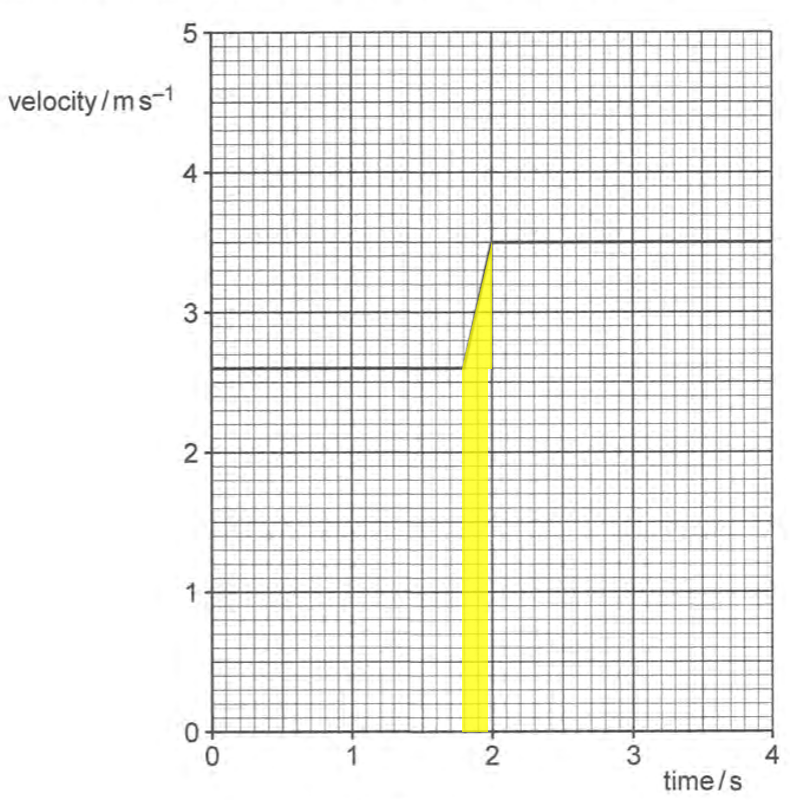
Area under the v-t graph\displaystyle =\frac{2.6+3.5}{2}\times 0.2=0.61\text{ m}

Leave a comment