22P2Q03

3a)

Since the field is uniform, the object experiences a force which is constant in both magnitude and direction (whether gravitational or electric), resulting in a constant downward acceleration.

Since the initial velocity is rightward, and acceleration is downward, the object moves in a parabolic path.

COMMENT: This is not a magnetic field!

3bi)

Gravitational force is attractive but electric force between like charges are repulsive.

3bii)

Electric force\displaystyle =k\frac{QQ}{{{r}^{2}}}=(8.99\times {{10}^{9}})\frac{{{(1.60\times {{10}^{-19}})}^{2}}}{{{r}^{2}}}\approx \frac{{{10}^{-28}}}{{{r}^{2}}}

Gravitational force\displaystyle =G\frac{MM}{{{r}^{2}}}=(6.67\times {{10}^{-11}})\frac{{{(9.11\times {{10}^{-31}})}^{2}}}{{{r}^{2}}}\approx \frac{{{10}^{-70}}}{{{r}^{2}}}

For the same separation, the electric force between two protons is much larger than the gravitational force between them. The two graphs are not drawn to the same scale.

3ci)

No. The electric field of P and R are both rightward at any point between them. For the two fields to cancel each other out, they must have opposite directions.

COMMENT: Electric field strength is a vector quantity.

3cii)

Yes. P produces a positive potential but R produces a negative potential. There is point between them where the two potentials sum to zero.

COMMENT: Electric potential is a scalar quantity.

3ciii)

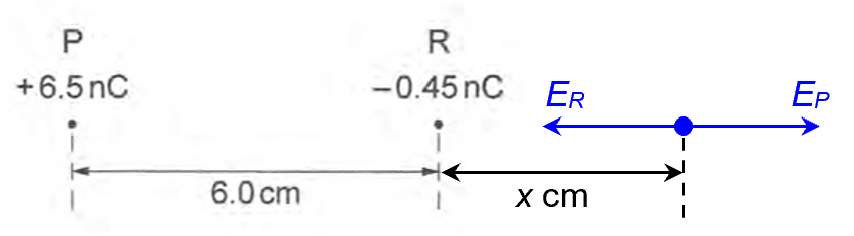
Let the null point be at x cm on the right of R.

At the null point,

\displaystyle \begin{aligned}   {{E}_{P}}&={{E}_{R}} \\  k\frac{6.5}{{{(6.0+x)}^{2}}}&=k\frac{0.45}{{{x}^{2}}} \\  \frac{x}{6.0+x}&=\sqrt{\frac{0.45}{6.5}} \\  x&=(6.0+x)(0.26312) \\  x&=2.14\text{ cm} \end{aligned}

Distance from P \displaystyle =6.0+2.14=8.14\text{ cm}

Leave a comment