4a)
If the spheres were oppositely charged, they would produce potentials of opposite signs. This would have resulted in a point between the spheres where the total potential is zero.
Both spheres must be positively charged since the potentials in the graph are all positive.
4b)
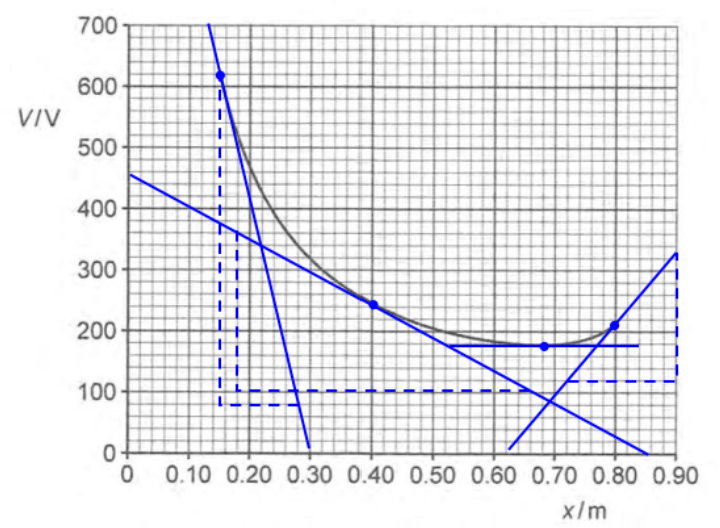
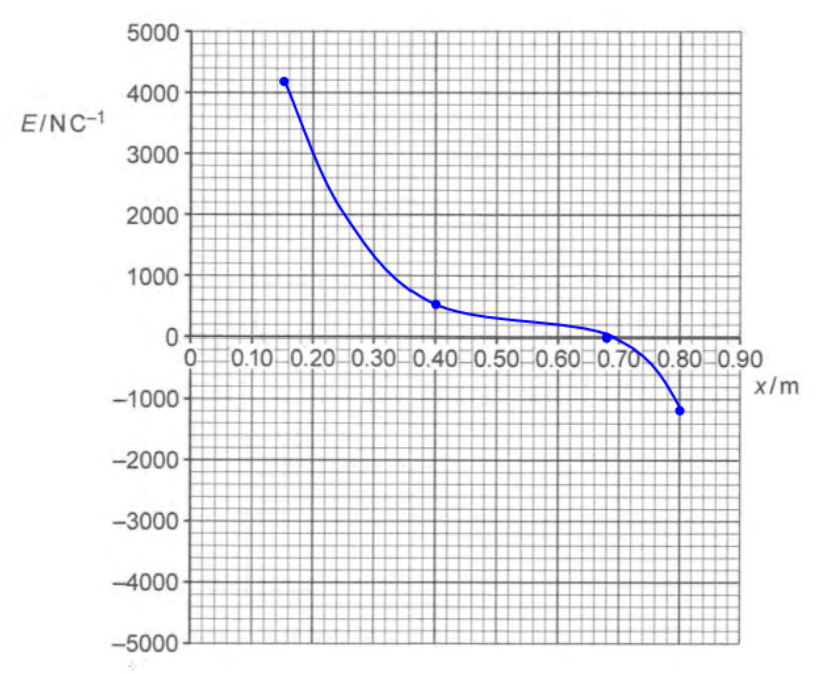
At ,
At ,
At ,
At ,
4ci)
4cii)
The actual electric potential on A’s surface is the summation of the electric potential due to both sphere A and B.
COMMENT: It is true that the charges on sphere A and B may not be uniformly distributed thanks to their mutual repulsion. However, this would have led to the charges moving further away from the point in the graph. This would only result in the value of V to be lower, not higher than what’s calculated.
COMMENT: Assuming the potential due to sphere B to be about 100 V at as the graph suggests, it would contribute about
to the potential at
.