23P3Q05

5a)

The gravitational potential at a point is the work done per unit mass

by an external force to bring a (small) mass from infinity to that point (without any change in KE of the

mass).

5b)

By principle of conservation of energy, the total KEi + GPEi when the projectile is on the surface of the planet, should be the same as the total KEf + GPEf when it is at the point at infinity.

\displaystyle \begin{aligned}  & K{{E}_{i}}+GP{{E}_{i}}=K{{E}_{f}}+GP{{E}_{f}} \\ & \frac{1}{2}m{{v}^{2}}+(-\frac{GMm}{R})=0+0 \\ & v=\sqrt{\frac{2GM}{R}} \end{aligned}

5ci)

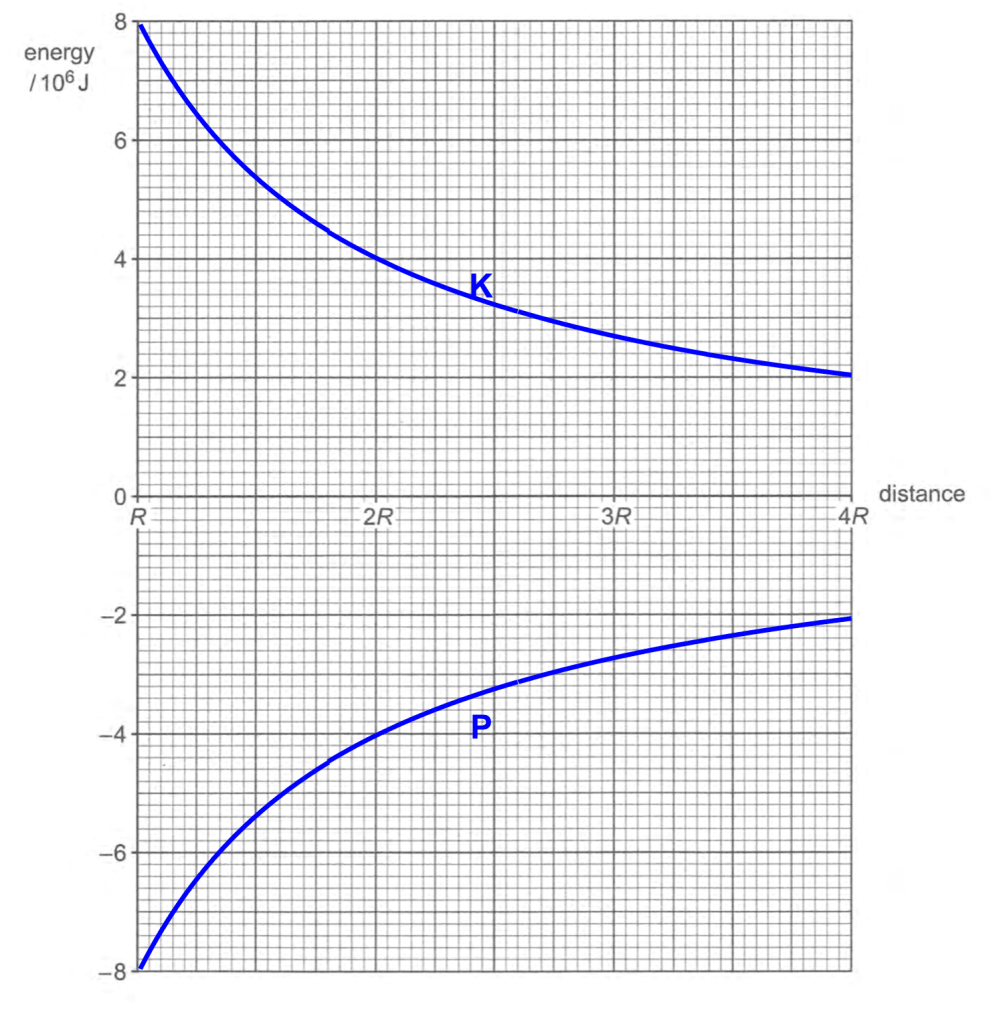
COMMENT: GPE + KE should be equal to zero, since the projectile just manages to escape. That’s how we deduced that GPE on the surface must be \displaystyle -8.0\times {{10}^{6}}\text{ J}.

COMMENT: Remember that gravitational potential is inversely proportional to distance.

COMMENT: Since GPE + KE is constant, the GPE and KE graphs are mirror images of each other.

2 thoughts on “23P3Q05”

  1. Pingback: A-Level 2023 – xmPhysics
  2. Pingback: A-Level 2024 – xmPhysics

Leave a comment