8ai)
8aii)
8aiii)
8b)
In order for the object to not go into oscillation, an upward external force must have supported the object as it is lowered.
The difference corresponds to the negative work done by this external force.
8c)
The magnitude of the restoring force is kx,
and it is directed towards the equilibrium position.
By newton’s second law:
8di)
COMMENT: Did you set your calculator to radian mode?
COMMENT: The negative sign means that object has swung to the other side.
8dii)
Method 1
Method 2
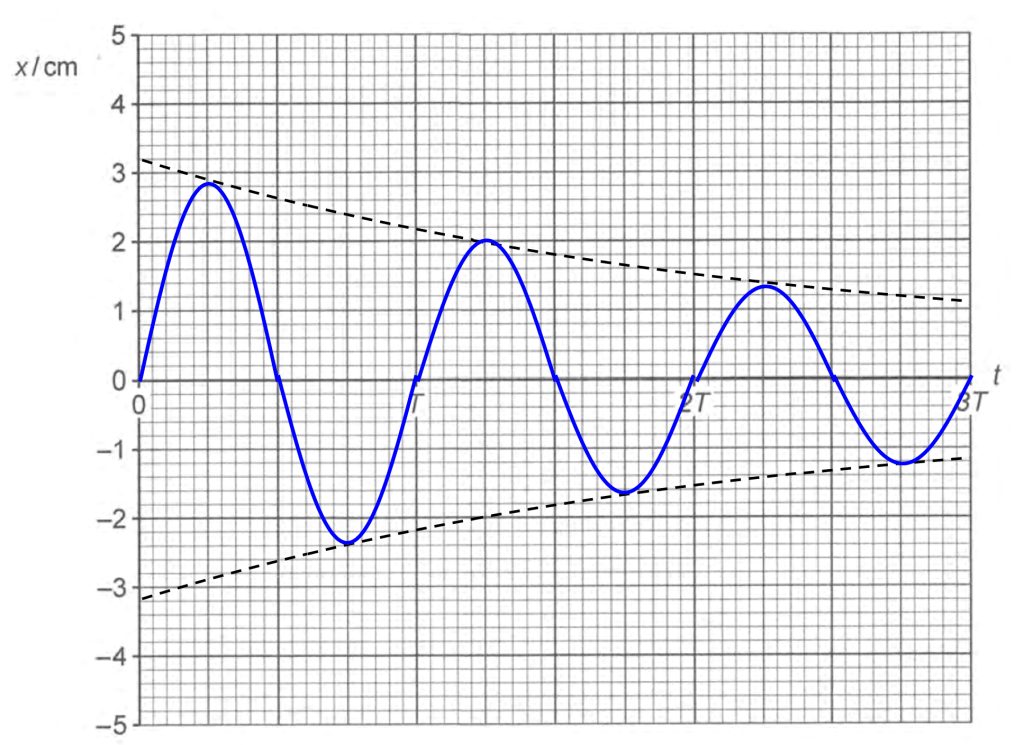
COMMENT: Graph must start from zero
COMMENT: Every amplitude must be lower than the previous one (on the other side of the graph).
COMMENT: We are assuming that the lengthening of period is negligible.
8fi)
Original and identical spring both have to support 3 N of weight.
The total extension is now doubled.
8fii)
The extension is now doubled for the same force, the effective spring constant is now halved,
Since , the new period is larger by a factor of
.
2 thoughts on “23P3Q08”