8ai)

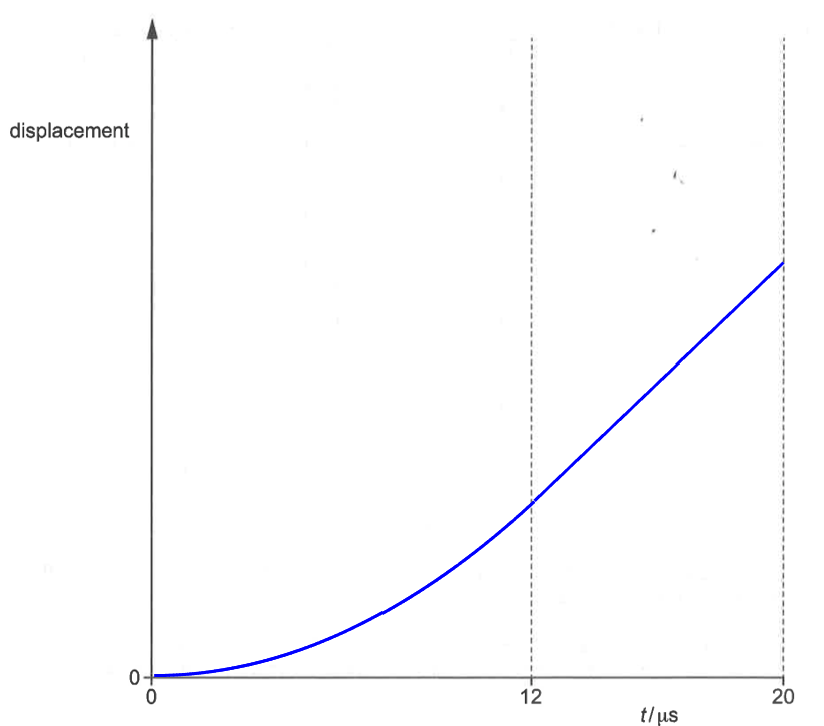
8aii)

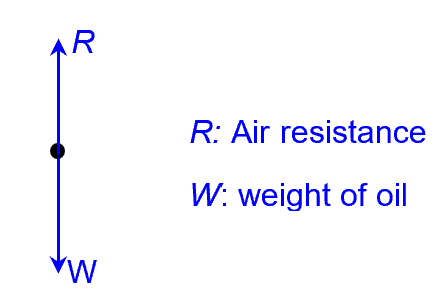
8bi)

COMMENT: For the electric force on a negative charge to be forward, the electric field should be downward.

8bii)

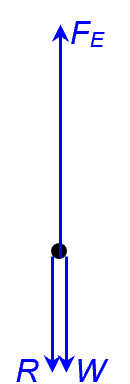
COMMENT: From part (a), we could infer that the magnitude of R when oil drop is moving at velocity of v₀ must be W. In part (b), since charge is now moving upward, R has switched direction to be downward. But the magnitude remains the same as W, since the oil drop is still moving at the same constant speed of v₀.

biii)

Hence 4 electrons transferred to oil drop.

8ci)

8cii)

Since the electric acceleration is initially much larger than g, the oil drop accelerates rightward almost horizontally.

As the oil drop moves further away from the oil drop, the electric field weaken rapidly and the acceleration decreases but has a larger downward component.

Eventually, the electric acceleration becomes negligible compared to g.

The oil drop then travels along a parabolic path, basically a projectile motion.

• Uncategorized