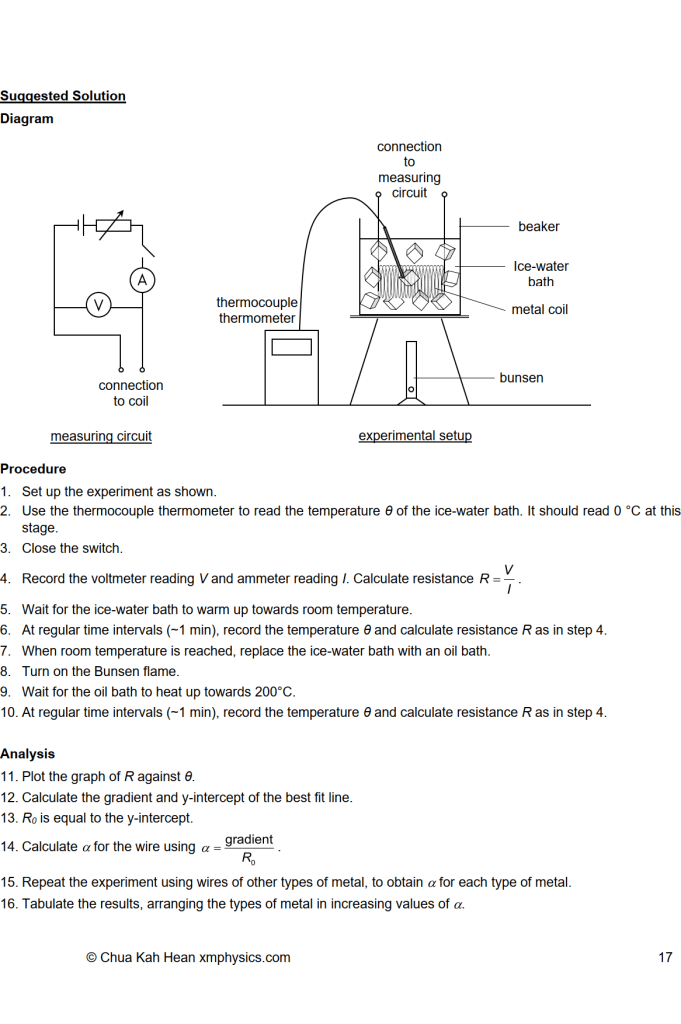
Author: mrchuakh

13P2Q08

12P2Q07

11P2Q07

10P2Q07

23P3Q09

9ai)

Decrease in mass after nuclear reaction

$\displaystyle \begin{aligned} \Delta m&=[400.19774-(393.54304+6.64466)]\times {{10}^{27}} \\ & =0.01004\times {{10}^{27}}\text{ kg} \end{aligned}$

Energy released $\displaystyle =\Delta m.{{c}^{2}}=(0.01004\times {{10}^{-27}}){{(3.00\times {{10}^{8}})}^{2}}=9.036\times {{10}^{-13}}\text{ J}$

9aii)

The total momentum of a system is constant if no net external force acts on it.

9aiii)

By PCOM, the momentum of the daughter nucleus and the alpha particle are equal but opposite. $\displaystyle {{p}_{D}}={{p}_{\alpha }}$

$\displaystyle \begin{aligned} \frac{K{{E}_{D}}}{K{{E}_{\alpha }}}&=\frac{{{p}_{D}}^{2}}{2{{m}_{D}}}\div \frac{{{p}_{\alpha }}^{2}}{2{{m}_{\alpha }}} \\ & =\frac{{{m}_{\alpha }}}{{{m}_{D}}} \\ K{{E}_{D}}&=\frac{4}{237}(8.784\times {{10}^{-13}}) \\ & =1.483\times {{10}^{-14}}\text{ J} \end{aligned}$

9aiv)

Perhaps a gamma photon is also released. So some of the energy released is with the gamma photon.

9bi)

$\displaystyle \begin{aligned} A&=\lambda N \\ 8130&=(5.08\times {{10}^{-11}})N \\ N&=1.60\times {{10}^{14}} \end{aligned}$

9bii)

$\displaystyle {{t}_{1/2}}=\frac{\ln 2}{\lambda }=\frac{\ln 2}{5.08\times {{10}^{-11}}}=1.36\times {{10}^{10}}\text{ s}$

9ci)

$\displaystyle A=\lambda N$

Activity is the product of the decay constant and the number of undecayed nuclei.

The beta emitter has a much higher initial activity since it has a higher decay constant, and the same initial number of undecayed nuclei.

9cii)

$\displaystyle A=\lambda N$

Initially, the activity of the beta emitter is higher than that of the americium-241.

However, as the number of beta emitters decrease more rapidly, the activity of the beta emitter will eventually be lower than that of the americium-241.

It takes americium-241 about 13 half-lives for its activity to decrease from 8130Bq to 1Bq. The beta emitter would have fallen to 1 Bq long before that.

COMMENT: The graph below depicts the situation if red sample has twice the decay constant as the blue. The two activities are equal within 1 half-life of the blue sample.

23P3Q08

8ai)

$\displaystyle k=\frac{F}{e}=\frac{4.00}{0.200}=20.0\text{ N }{{\text{m}}^{-1}}$

8aii)

$\displaystyle EPE=\frac{1}{2}Fe=\frac{1}{2}(3.0)(0.15)=0.225\text{ J}$

8aiii)

$\displaystyle \Delta GPE=mg\Delta h=(3)(0.15)=0.45\text{ J}$

8b)

In order for the object to not go into oscillation, an upward external force must have supported the object as it is lowered.

The difference corresponds to the negative work done by this external force.

8c)

The magnitude of the restoring force is kx,

and it is directed towards the equilibrium position.

By newton’s second law:

$\displaystyle \begin{aligned} & ({{F}_{net}}=ma) \\ & -kx=ma \\ & a=-\frac{k}{m}x \end{aligned}$

8di)

$\displaystyle \begin{aligned} \omega &=\sqrt{\frac{k}{m}} \\ &=\sqrt{\frac{20.0}{3\div 9.81}} \\ &=8.087\text{ rad }{{\text{s}}^{-1}} \end{aligned}$

$\displaystyle \begin{aligned} (x&={{x}_{0}}\sin \omega t) \\ x&=3.2\sin (8.087\times 0.50) \\ &=-2.51\text{ cm} \end{aligned}$

COMMENT: Did you set your calculator to radian mode?

COMMENT: The negative sign means that object has swung to the other side.

8dii)

Method 1

$\displaystyle \begin{aligned} (v&={{v}_{\max }}\cos \omega t) \\ v&=(8.087)(3.2)\cos (8.087\times 0.50) \\ &=-16.0\text{ cm }{{\text{s}}^{-1}} \end{aligned}$

Method 2

$\displaystyle \begin{aligned} v&=\pm \omega \sqrt{{{x}_{0}}^{2}-{{x}^{2}}} \\ &=\pm 8.087\sqrt{{{3.2}^{2}}-{{(-2.51)}^{2}}} \\ &=\pm 16.1\text{ cm }{{\text{s}}^{-1}} \end{aligned}$

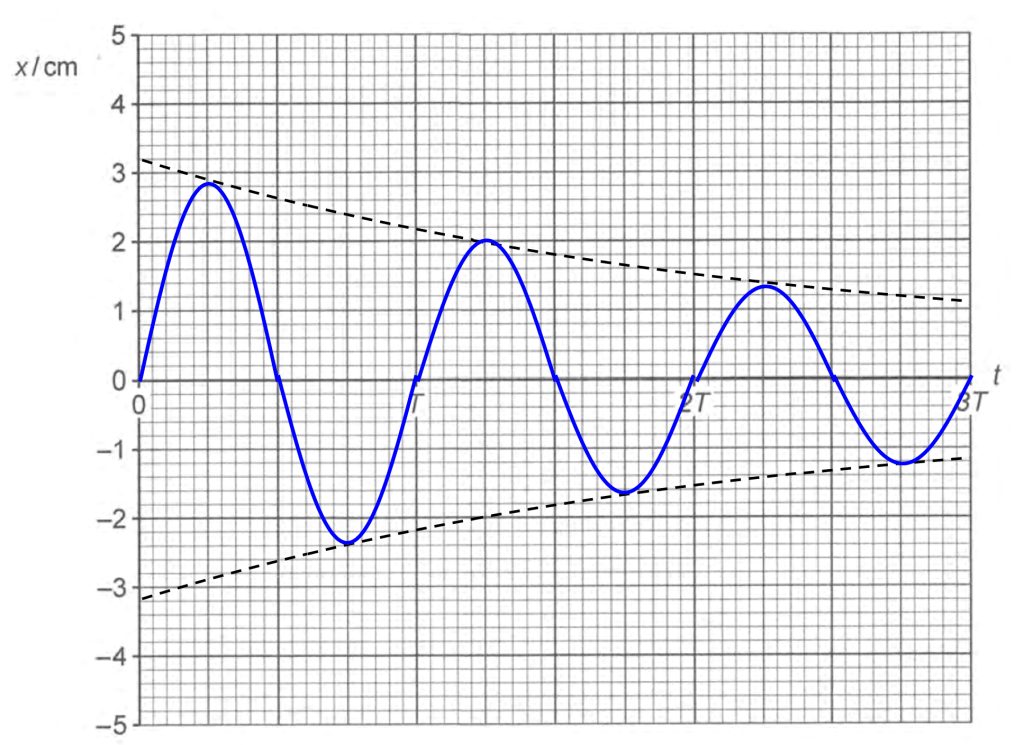
COMMENT: Graph must start from zero

COMMENT: Every amplitude must be lower than the previous one (on the other side of the graph).

COMMENT: We are assuming that the lengthening of period is negligible.

8fi)

Original and identical spring both have to support 3 N of weight.

The total extension is now doubled.

8fii)

The extension is now doubled for the same force, the effective spring constant is now halved,

Since $\displaystyle \omega =\sqrt{\frac{k}{m}}$ , the new period is larger by a factor of $\displaystyle \sqrt{2}$ .

23P3Q07

7a)

Electric field strength at a point is the force per unit positive charge acting on a small test charge

placed at that point.

7bi)

COMMENT: Equally space lines, arrows pointing inwards, ending perpendicularly on the surface of the sphere.

7bii)

$\displaystyle \begin{aligned} & (E=k\frac{Q}{{{r}^{2}}}) \\ & 130=(8.99\times {{10}^{9}})\frac{Q}{{{(0.15+0.40)}^{2}}} \\ & =4.37\times {{10}^{-9}}\text{ C} \end{aligned}$

23P3Q06

6ai)

COMMENT: The mean KE is directly proportional to the kelvin temperature.

6aii)

0.25

COMMENT: Think $\displaystyle \frac{PV}{T}=nR$

6aiii)

Since they have the same mean KE,

$\displaystyle \begin{aligned} & \frac{1}{2}(m){{c}_{A}}^{2}=\frac{1}{2}(2m){{c}_{B}}^{2} \\ & \frac{{{c}_{A}}}{{{c}_{B}}}=\sqrt{2} \end{aligned}$

6b)

R.m.s. speed of the molecules in container A, $\displaystyle {{c}_{A}}=\sqrt{2}(940)=1329\text{ m }{{\text{s}}^{-1}}$

Mass of a molecule in container A, $\displaystyle m=\frac{{{M}_{molar}}}{{{N}_{A}}}=\frac{4.0\times {{10}^{-3}}}{6.02\times {{10}^{23}}}=6.645\times {{10}^{-27}}\text{ kg}$

$\displaystyle$

$\displaystyle \begin{aligned} \left\langle KE \right\rangle &=\frac{3}{2}kT \\ \frac{1}{2}m{{c}_{A}}^{2}&=\frac{3}{2}kT \\ (6.645\times {{10}^{-27}}){{(1329)}^{2}}&=3(1.38\times {{10}^{-23}})T \\ T&=283\text{ K} \end{aligned}$

23P3Q05

5a)

The gravitational potential at a point is the work done per unit mass

by an external force to bring a (small) mass from infinity to that point (without any change in KE of the

mass).

5b)

By principle of conservation of energy, the total KE_i + GPE_i when the projectile is on the surface of the planet, should be the same as the total KE_f + GPE_f when it is at the point at infinity.

$\displaystyle \begin{aligned} & K{{E}_{i}}+GP{{E}_{i}}=K{{E}_{f}}+GP{{E}_{f}} \\ & \frac{1}{2}m{{v}^{2}}+(-\frac{GMm}{R})=0+0 \\ & v=\sqrt{\frac{2GM}{R}} \end{aligned}$

5ci)

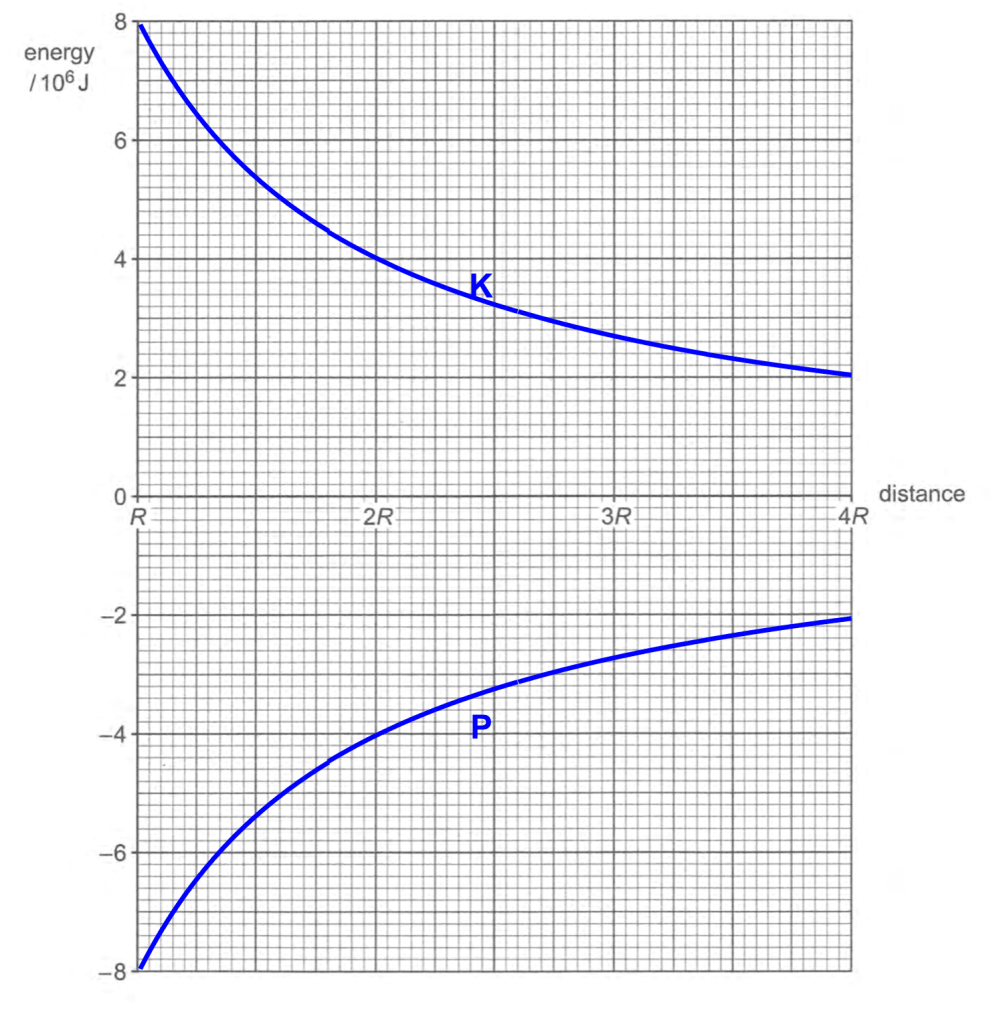
COMMENT: GPE + KE should be equal to zero, since the projectile just manages to escape. That’s how we deduced that GPE on the surface must be $\displaystyle -8.0\times {{10}^{6}}\text{ J}$ .

COMMENT: Remember that gravitational potential is inversely proportional to distance.

COMMENT: Since GPE + KE is constant, the GPE and KE graphs are mirror images of each other.

23P3Q04

4a)

The magnetic flux density at a point in a magnetic field is the force per unit length per unit current

acting on a straight current-carrying conductor placed perpendicular to the field.

4bi)

The rod is experiencing a magnetic force because it is carrying a current and placed perpendicular to the magnetic field.

The balance reading decreased because a magnetic force now helping to support the magnet’s weight.

This means that the magnetic force acting on the magnet must be upward.

By Newton’s 3^rd Law, the magnetic force acting on the wire must be downward.

With the magnetic field directed from N to S, the current in the rod must be from X to Y. (FLHR)

4bii)

Change in mass reading $\displaystyle \Delta m=\frac{202.17-201.62}{2}=0.275\text{ g}$

The change is due to the magnetic force: $\displaystyle \begin{aligned} & \Delta mg=BIL \\ & (0.275\times {{10}^{-3}})(9.81)=B(1.60)(0.12) \\ & B=1.41\times {{10}^{-2}}\text{ T} \end{aligned}$

4biii)

No change.

Since the change in magnetic force is same as before, the change in mass reading is also same as before.

COMMENT: The mass of the rod is irrelevant. It only plays the part of exerting the magnetic force on the magnet.