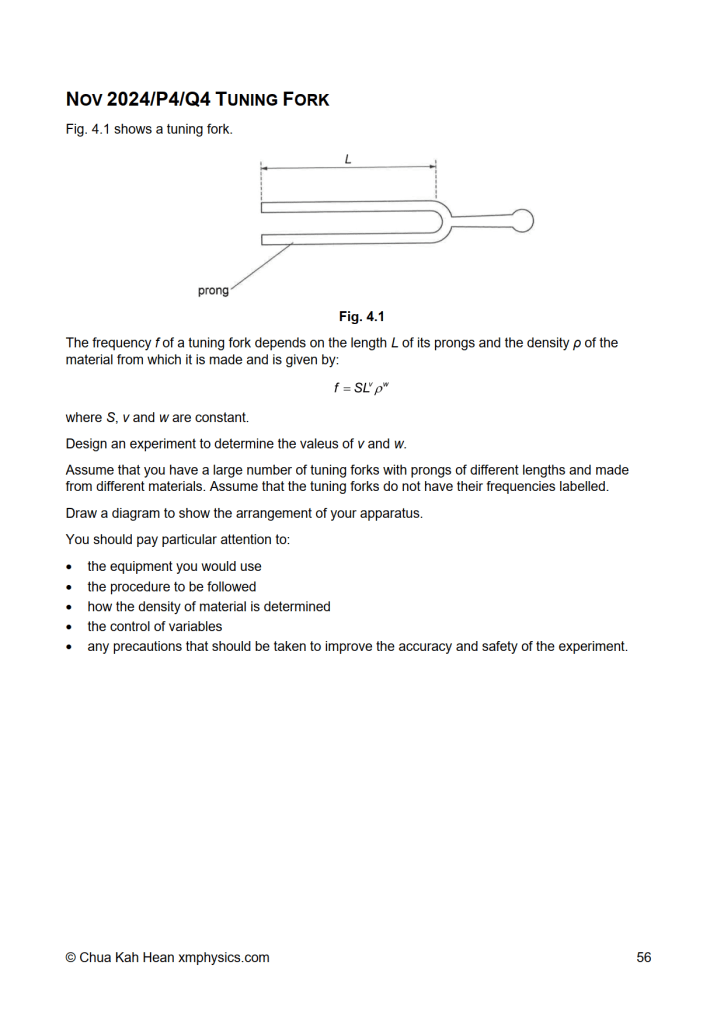
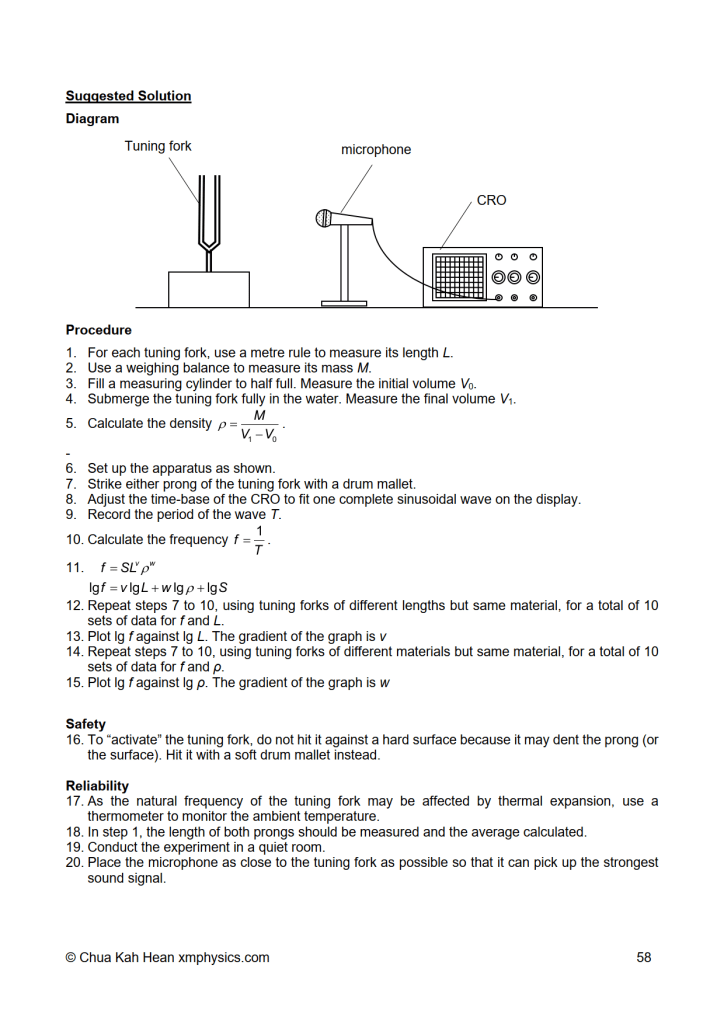
Category: Uncategorized
8ai)
8aii)
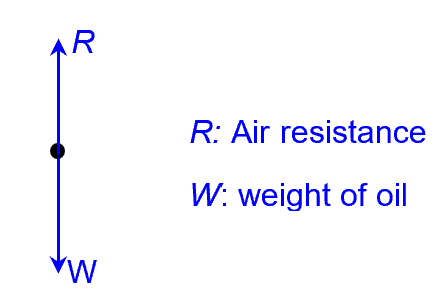
8bi)
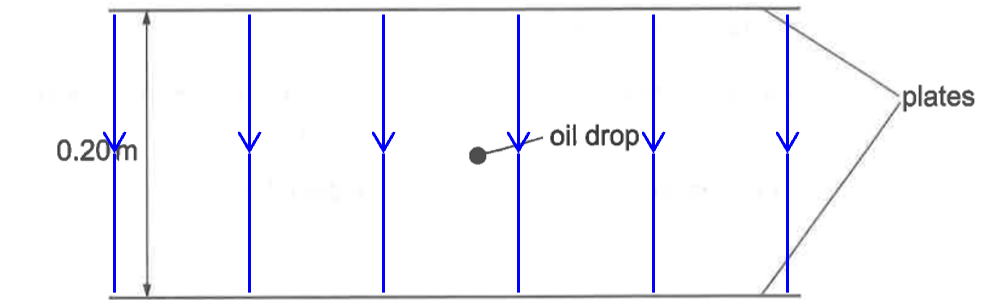
COMMENT: For the electric force on a negative charge to be forward, the electric field should be downward.
8bii)
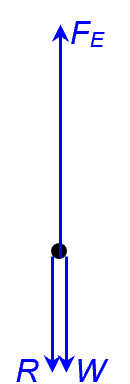
COMMENT: From part (a), we could infer that the magnitude of R when oil drop is moving at velocity of v0 must be W. In part (b), since charge is now moving upward, R has switched direction to be downward. But the magnitude remains the same as W, since the oil drop is still moving at the same constant speed of v0.
biii)
Hence 4 electrons transferred to oil drop.
8ci)
8cii)
Since the electric acceleration is initially much larger than g, the oil drop accelerates rightward almost horizontally.
As the oil drop moves further away from the oil drop, the electric field weaken rapidly and the acceleration decreases but has a larger downward component.
Eventually, the electric acceleration becomes negligible compared to g.
The oil drop then travels along a parabolic path, basically a projectile motion.
6a)
Similarity: Both refer to energy converted per unit charge, measured in volts.
Difference: Whie e.m.f. is about conversion from non-electrical to electrical forms by a battery, p.d. is about conversion from electrical to non-electrical forms in the external circuit.
6bi)
The voltmeter is not measuring the e.m.f. but the terminal p.d. of the battery.
Since a current is flowing, there is p.d. across the internal resistance of the battery, making the terminal p.d. smaller than the e.m.f.
6bii)
Total resistance
P.d. across the 10 Ω
6ci)
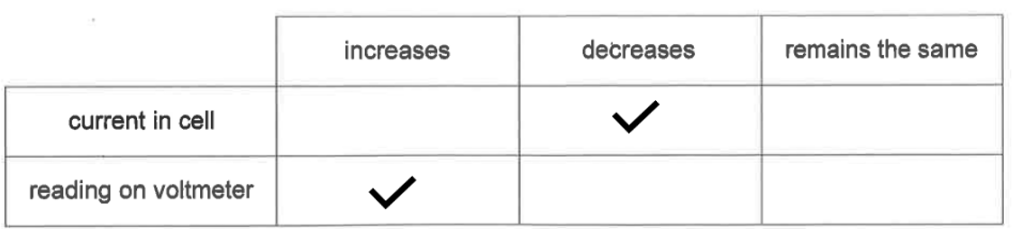
6cii)
First, solve for the internal resistance of battery r.
Effective resistance across the 10 Ω
By P.D.P., p.d. across the 10 Ω
9ai)
When two (or more) waves overlap, the resultant displacement (at any point and instant) is the (vector) sum of the displacements due to each individual wave (at that point and instant).
9aii)
Light waves with constant phase difference(s).
9bi)
1.5λ
COMMENT: The first minima occurs where path difference is 0.5λ. The second minima occurs where path difference is 1.5λ.
9bii)
The path difference at R is 1.5λ, which is an odd number of half wavelengths.
The light waves from A and B therefore superpose in anti-phase at R, resulting in a destructive interference.
9biii)
9biv)
Since the double slits are also two single slits, the resulting interference pattern is a combination of both double-slit and a single-slit interference pattern.
As a single slit, a central maximum would have been formed, with intensity peaking at the centre, and decreases along either sides.
As a result, the intensity of the bright fringes formed by double-slit interference will also peak at the centre, and decreases along either sides.
COMMENT: The intensity of the double-slit interference fringes is modulated by the single-slit diffraction envelope.
c)
Light from slit A has intensity I and amplitude A.
Light from slit B has intensity and amplitude
.
Amplitude at P has amplitude .
Intensity at P is thus
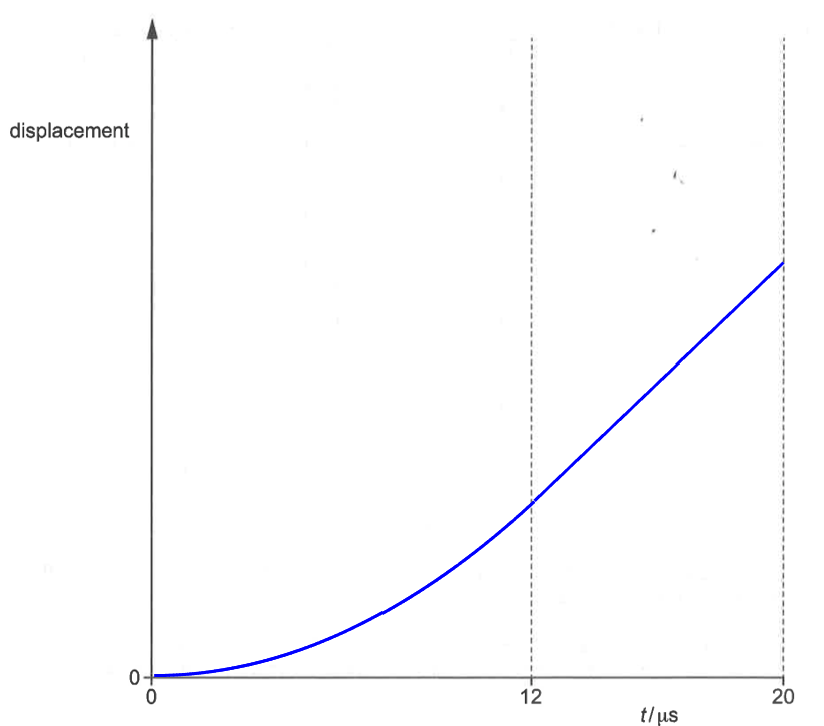
di)
dii)
Assuming 2.9 mm and 1.12 m are both measured using the same instrument with the same resolution, the percentage uncertainty of 2.9 mm is much higher than that of 1.12m.
7a)
Think of the tube as consisting of many circular rings.
As the magnetised steel block moves through each ring, the ring experiences a changing magnetic flux linkage. Hence e.m.f is induced around the ring.
Since copper is a conductor, an induced current follows.
The induced current results in a magnetic force on the steel block. By Lenz’s law, the magnetic force must always act upward to retard the motion of the steel block, which is the cause of induction.
5a)
5bi)
5bii)
5biii)