An electric charge in an electric field always experiences an electric force. A charge in a magnetic field, however, does not necessarily experience a magnetic force.

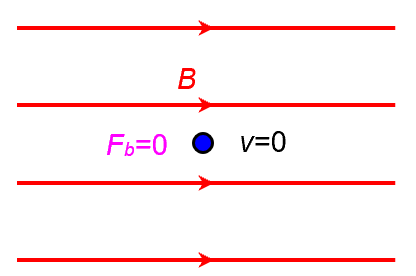
Stationary Charge

Just like a wire carrying zero current experiences no magnetic force, a stationary charge does not experience any magnetic force. This is because and . In the absence of other forces, this charge simply remains at rest.

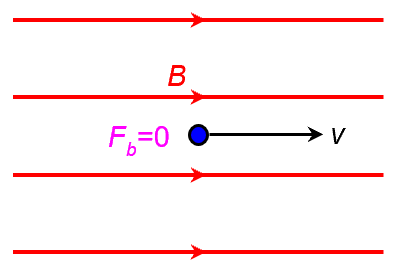
v parallel to B

Just like a current carrying conductor placed parallel to a magnetic field experiences no magnetic force, a charge moving parallel to the direction of B does not experience any magnetic force. This is because and . In the absence of other forces, this charge simply continues moving at velocity v.

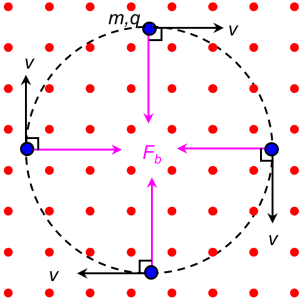
v perpendicular to B

A charge moving perpendicular to the direction of B, however, does experience the magnetic force . It is important you realize that F_b is always perpendicular to v no matter how v rotates and turns. If F_b is the only force acting on this charge, this charge will be traveling along a circular path![1]

For a particle of mass m and charge q, we have

To find T, the time taken for one complete revolution, we can divide the distance by speed:

Two interesting results:

1. For the same v and B, the radius of circular motion is directly proportional to , the mass to charge ratio. This relationship is the basis for mass spectroscopy.
2. The time taken for a charged particle to complete one revolution is independent of its speed. This result is exploited in the design of particle accelerators called cyclotrons.

–

Demonstration

CRT Magic

Magnetic Pump

Concept Test

2836

---

[1] This is not so for the electrons drifting in a current-carrying conductor because they are constrained by the metallic bonds to drift inside the wire.

• Uncategorized